Machine learning cơ bản với Python #Bài 03

BÀI 3. HỒI QUY TUYẾN TÍNH, HỒI QUY ĐA THỨC VÀ HỒI QUY ĐA BIẾN

Thuật ngữ hồi quy được sử dụng khi chúng ta cố tìm quan hệ giữa các biến với nhau
Trong Machine learning, và trong các mô hình thống kê, các mối quan hệ đó được sử dụng để dự đoán kết quả của các sự kiện trong tương lai.

3.1. HỒI QUY TUYẾN TÍNH
Hồi quy tuyến tính (Linear regression) sử dụng quan hệ giữa các điểm dữ liệu để vẽ một đường thẳng. Đường thẳng này được sử dụng để dự đoán giá trị tương lai.

Trong Machine learning, dự đoán tương lại là rất quan trọng

Python có các cách để tìm tương quan giữa các điểm dữ liệu và để vẽ đường thẳng của hồi quy tuyến tính. Chúng ta sẽ dùng những cách này thay vì tìm công thức toán học để vẽ đường thẳng hồi quy đó.

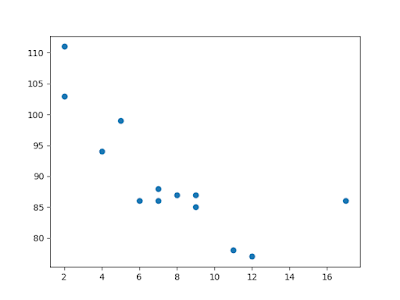
Trong ví dụ dưới đây, trục x thể hiện tuổi đời, trục y thể hiện tốc độ. Chúng ta sẽ xem liệu những dữ liệu này có thể sử dụng trong hồi quy tuyến tính?

import matplotlib.pyplot as plt
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
plt.scatter(x, y)
plt.show()

Kết quả

Sử dụng thêm các hàm để vẽ hồi quy tuyến tính cho dữ liệu trên

import matplotlib.pyplot as plt
from scipy import stats

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

slope, intercept, r, p, std_err = stats.linregress(x, y)

def myfunc(x):
return slope * x + intercept

mymodel = list(map(myfunc, x))

plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()

Và chúng ta được kết quả là đường thẳng như sau

Giải thích các hàm sử dụng ở trên
- import module cần thiết gồm: matplotlib và stats
  import matplotlib.pyplot as plt
from scipy import stats
- Tạo arrays thể hiện giá trị trục x và y
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

- Thực hiện các giá trị quan trọng của hồi quy tuyến tính gồm: slope, intercept, r, p, std_err
  slope, intercept, r, p, std_err = stats.linregress(x, y)

- Tạo function sử dụng giá trị slope và intercept để trả về giá trị mới. Giá trị mới này thể hiện vị trí trên trục y tương ứng với giá trị trên trục x.

def myfunc(x):
  return slope * x + intercept

- Chạy từng giá trị của trục x qua function. Cho kết quả trên array mới với giá trị mới trên trục y

mymodel = list(map(myfunc, x))

- Vẽ đồ thị scatter và vẽ đường hồi quy tuyến tính, sau đó thể hiện trên biểu đồ

plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()

R-Squared (R2)

Khi chúng ta tìm tương quan, một hệ số rất quan trọng là R2, nó thể hiện mối liên hệ giữa 2 đại lượng. Nếu chúng không có mối tương quan nào, thì đường hồi quy tuyến tính không thể sử dụng để dự đoán cho tương lai.

Giá trị R-squared nằm trong khoảng [0-1], trong đó 0 nghĩa là không tương quan và 1 nghĩa là 100% tương quan

Python và module Scipy sẽ tính giá trị R2 cho chúng ta, chúng ta chỉ cần in nó ra là được

from scipy import stats

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

slope, intercept, r, p, std_err = stats.linregress(x, y)

print(r)

Kết quả r = 0.76, không hoàn hảo lắm, nhưng nó chỉ ra rằng, chúng ta có thể sử dụng để dự đoán tương lai.

Dự đoán giá trị tương lai

Bây giờ, chúng ta sử dụng thông tin chúng ta tập hợp được để dự đoán các giá trị tương lai

Ví dụ, dự đoán tốc độ của 1 chiếc xe 10 năm tuổi, chúng ta cần sử dụng hàm myfunc() từ ví dụ trên

from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

slope, intercept, r, p, std_err = stats.linregress(x, y)

def myfunc(x):
return slope * x + intercept

speed = myfunc(10)

print(speed)

Kết quả là 85.6, chúng ta có thể tính gần đúng bằng mắt thường thông qua biểu đồ

3.2. HỒI QUY ĐA THỨC - POLYNOMIAL REGRESSION
Nếu dữ liệu điểm của bạn không thể nào fit được với hồi quy tuyến tính, thì bạn nên nghĩ đến hồi quy đa thức.
Hồi quy đa thức, cũng như hồi quy tuyến tính, sử dụng quan hệ giữa biến x và y để tìm cách nhất vẽ một đường (cong hoặc thẳng) qua các điểm dữ liệu.

Định nghĩa hồi quy đa thức: (nguồn kiwimedia tiếng Anh) "Trong thống kê, hồi quy đa thức là một dạng phân tích hồi quy trong đó mối quan hệ giữa biến độc lập x và biến phụ thuộc y được mô hình hóa như một đa thức bậc n trong x"

Thông thường, ta phải đi tìm công thức để có được đường cong phù hợp với dữ liệu, nhưng rất hên là Python có cách để tìm mới quan hệ đó để vẽ được đường hồi quy đa thức. Việc của chúng ta là gọi công thức đó ra và bảo nó làm cho mình, quá sướng.

Hãy bắt đầu với ví dụ sau đây:
trục x là thời gian (tính bằng giờ) 1 chiếc xe đi qua trạm thu phí
trục y là tốc độ của nó khi đi qua trạm thu phí
(thu phí tự động, không dừng trả tiền nhé :D)

import matplotlib.pyplot as plt

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

plt.scatter(x, y)
plt.show()

Sau đó, chúng ta sẽ import numpy và matlotlib, để vẽ đường hồi quy đa thức

import numpy
import matplotlib.pyplot as plt

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

myline = numpy.linspace(1, 22, 100)

plt.scatter(x, y)
plt.plot(myline, mymodel(myline))
plt.show()

Hãy cùng phân tích code python ở trên nhé
- Cũng giống như phần 3.1, chúng ta cần import các module numpy và matplotlib
import numpy
import matplotlib.pyplot as plt
- Tạo arrays thể hiện giá trị x, y
x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

- Dùng lệnh poly1d trong numpy để vẽ đường cong
mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

- Sau đó chi tiết hóa đường cong, chúng ta sẽ bắt đầu tại vị trí số 1 và kết thúc tại vị trí số 22

myline = numpy.linspace(1, 22, 100)

- Vẽ biểu đồ scatter gốc, đường hồi quy và thể hiện trên biểu đồ
plt.scatter(x, y)
plt.plot(myline, mymodel(myline))
plt.show()

R-Squared (R2)

Để tính chỉ số R2 (hiểu là R bình phương nhé, tại trong này khó viết số mũ quá) chỉ cần print nó ra với lệnh

print(r2_score(y, mymodel(x)))

Kết quả, R2 = 0.94

Con số này rất ấn tượng, nó thể hiện rằng đường hồi quy của mình có tương quan rất tốt, và ta có thể sử dụng nó để dự đoán cho tương lai.

Dự đoán giá trị tương lai

Bây giờ chúng ta sẽ dự đoán tốc độ 1 chiếc xa đi qua trạm thu phí lúc 17:00 PM

import numpy
from sklearn.metrics import r2_score

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

speed = mymodel(17)
print(speed)

Kết quả là 88.87, ta có thể ước lượng được giá trị đó trên biểu đồ